Límites laterales de manera analítica.
Como se vio en la sección dos de este capítulo si el límite de una función en un punto \(x=c\) existe está condicionado a que los límites por la izquierda y por la derecha existan y tiendan al mismo valor, lo cual se escribe, $$\lim_{x \to c^-}{f(x)}=L=\lim_{x \to c^+}{f(x)}$$ Estos límites se conocen como límites laterales y cumplen con todas las propiedades de los límites ya expresadas. Su uso analítico en el cálculo está condicionado a algunos casos en los cuales solo se desea conocer el límite de una función por la izquierda o la derecha de algún valor, ya sea porque no se puede determinar por el otro lado o simplemente porque no interesa. Ver los ejercicios del uno al cuatro.
Para más contenidos clic en y luego clic en la pestaña del contenido deseado.
Límites al infinito y asíntotas de funciones racionales.
Comience por recordar el concepto de infinito, en ocasiones una función crece o decrece sin parar y se hace necesario de una notación especial que permita la discusión de una manera apropiada. Para tales casos las matemáticas se valen del concepto de infinito representado por una lemniscata \(\infty.\)
Al decir que una cantidad \(x\) crece o decrece sin límites, o que puede tomar infinitos valores se expresa “\(x\) tiende a infinito” lo cual se escribe como \(x\to\infty\), pero tenga en cuenta que infinito no es número, por tanto, carece de sentido pensar que \(\infty+\infty=2\infty,\) más aún pensar que \(\infty-\infty=0,\) tales afirmaciones son incorrectas y desafían la lógica.
Al analizar límites de manera gráfica se vio la inexistencia del $$\lim_{x\to0}{\frac{5}{x^2}},$$ en realidad todas las funciones de la forma \(f\left(x\right)=\frac{k}{x^2}\) para \(k>0\) tienen el mismo comportamiento en cuanto a su gráfica (crecen al infinito) a medida que \(x\) tiende a cero por ambos lados. Este hecho puede escribirse como, $$\lim_{x\to0}{\frac{k}{x^2}}=\infty ~~{\rm para~~} k>0$$ En ninguna manera la afirmación anterior expresa que el límite exista, ya que infinito \(\infty\) no es un número, pero ofrece una idea analítica del comportamiento de la función sin la necesidad de realizar un boceto de su gráfica. A medida que \(x\) tiende a cero, la función se hace más y más grande o más y más pequeña si \(k< 0.\)
De igual modo ciertas funciones pueden tener límites laterales (por la izquierda o por la derecha), cuyos resultados sean infinito o menos infinito, en cuyo caso se puede tener una o varias de las siguientes afirmaciones: \begin{array}{l l} 1.\lim_{x\to c^-}{f(x)}=\infty\ \ & 2.\lim_{x \to c^-}{f(x)}=-\infty\\ 3.\lim_{x\to c^+}{f(x)}=\infty\ \ & 4.\lim_{x \to c^+}{f(x)}=-\infty\end{array} Geométricamente el significado de que el límite va al finito (o menos infinito) es una asíntota vertical para la gráfica de la función en el punto dado, como se explica a continuación.
Asíntotas verticales.
Se dice que una función \(f(x)\) tiene un comportamiento asintótico, cuando a medida que \(x\) se aproxima (tiende) a un valor, la función crece o decrece sin límite. Dada \(f\left(x\right)\) una función racional de la forma,
$$f\left(x\right)=\frac{p\left(x\right)}{q\left(x\right)}=\frac{a_mx^m+a_{m-1}x^{m-1}+\ldots+a_1x^1+a_0}{b_nx^n+b_{n-1}x^{n-1}+\ldots+b_1x^1+b_0}$$
definida para algún intervalo de \(\mathbb{R},\) se puede tener tres tipos de asíntotas, horizontales, verticales y oblicuas, para la gráfica de \(f(x)\) según sea el caso.
Definición de asíntota vertical.
La recta \(x=c\) es una asíntota vertical de la gráfica \(y=f\left(x\right)\) si y solo si, al menos una de las afirmaciones siguientes es verdadera.
\begin{array}{l}
1.\lim_{x\to c}{f(x)}=-\infty \ \ \ \ \ \ {\rm ó} \ \ \ \ \ 2. \lim_{x\to c}{f(x)}=\infty\\
3.\lim_{x\to c^-}{f(x)}=-\infty \ \ \ \ \ {\rm ó} \ \ \ \ \ 4.\lim_{x\to c^-}{f(x)}=\infty\\
5.\lim_{x\to c^+}{f(x)}=-\infty \ \ \ \ \ {\rm ó} \ \ \ \ \ 6.\lim_{x\to c^+}{f(x)}=\infty\end{array}
Las asíntotas verticales si las hay, están en los puntos que hacen cero el denominador, pero no el numerador.
Dado que para el denominador
$$q\left(x\right)=b_nx^n+b_{n-1}x^{n-1}+\ldots+b_1x^1+b_0$$ existe un número finitos de puntos \(x=c\) para los cuales \(q\left(c\right)=0,\) el número de asíntotas verticales para una función racional (si las hay) es finito.
Ver los ejercicios nueve y diez de los Ejercicios I.
Límites al infinito.
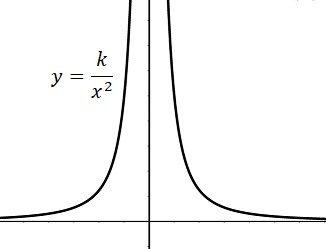 Considere nuevamente la gráfica de la función \(f(x)=\frac{k}{x^2}\) de la figura de la izquierda, como se vio, la misma presenta una asíntota vertical en \(x=0.\) Sin embargo, una función \(f\) puede tener otros tipos de comportamientos asintóticos al acercase a un determinado valor.
Considere nuevamente la gráfica de la función \(f(x)=\frac{k}{x^2}\) de la figura de la izquierda, como se vio, la misma presenta una asíntota vertical en \(x=0.\) Sin embargo, una función \(f\) puede tener otros tipos de comportamientos asintóticos al acercase a un determinado valor.
Considere la gráfica de \(y=f(x)\) y la recta \(y=0\) como se muestra en la figura de la arriba. A medida que \(x\) crece sin límite, la gráfica de la función \(y=f(x)\) se acerca más y más (tiende) a la gráfica de la recta \(y=0.\) Este resultado se expresa analíticamente como $$\lim_{x\to\infty}{f(x)}=0.$$ Sin embargo, observe también que a medida que \(x\) decrece sin límites la gráfica de \(f(x)\) se acerca más y más (tiende) a la recta \(y=0.\) Este resultado se expresa analíticamente como $$\lim_{x\to{-\infty}}{f(x)}=0.$$ Aunque infinito no es un número, puede enunciarse el resultado como sigue.
Definición formal de límites al infinito.
Sea \(f(x)\) una función cualquiera definida para \(\left(-\infty,a\right)\) o \(\left(b,\infty\right)\) entonces afirmar que, $$\lim_{x\to{-\infty}}{f(x)}=L\ \ {\rm o} \ \ \lim_{x\to\infty}{f(x)}=L$$ quiere decir que \(f(x)\) se aproxima a la recta \(y=L\) tanto como se desee, al hacer \(x\) tan grande o pequeña como se pretenda.
De la definición épsilon-delta del límite se vio que la expresión $$\lim_{x\to c}{f(x)}=L$$ significa que para todo \(\varepsilon>0\) existe un \(\delta>0\) tal que \(0<\left|x-c\right|<\delta\) siempre que \(\left|f\left(x\right)-L\right|<\varepsilon.\) De igual manera se puede enunciar una definición épsilon-delta para el límite cuando \(x\rightarrow\infty\) aun cuando infinito representa una idealización numérica como sigue.
Límites al infinito.
1. \(\lim_{x\to\infty}{f\left(x\right)}=L\) expresa que para todo \(\varepsilon>0\) existe un \(k>0\) tal que \(\left|f\left(x\right)-L\right|< \varepsilon\) siempre que \(x>M.\)
2. \(\lim_{x\to\infty}{f\left(x\right)}=L\)
expresa que para todo \(\varepsilon>0\) existe un \(K< 0\) tal que \(\left|f\left(x\right)-L\right|<\varepsilon\) siempre que \(x < k.\)
Determinación de límites al infinito
Para la determinación de límites al infinito de manera analítica, se aplican las misma reglas y propiedades para los límites cuando \(x\rightarrow c\) teniendo en cuenta la afirmación siguiente.
Limites al infinito
Sea \(k\in\mathbb{R}\) y \(r\in\mathbb{Q}^+\) si \(x^r\) está definida para toda \(x\) entonces, $$\lim_{x\to\infty}{\frac{k}{x^r}}=0\ \ y\ \lim_{x\to-\infty}{\frac{k}{x^r}}=0$$
Estrategias para el cálculo de límites al infinito.
Además de las propiedades de los límites y el uso del álgebra para reescribir las funciones como otra función que coincida con ella salvo en un punto, las estrategias siguientes facilitan el cálculo de límites que tienden al infinito.
Estrategia E1. Si la función es de la forma \(f\left(x\right)=\sqrt{p(x)}\) factorizar la mayor potencia de \(x\) dentro del radical, simplificar la función y aplicar propiedades de límites para calcular el límite.
Estrategía E2. Si \(f(x)\) es una función racional tal que, $$f(x)=\frac{a_mx^m+a_{m-1}x^{m-1}+\ldots+a_1x^1+a_0}{b_nx^n+b_{n-1}x^{n-1}+\ldots+b_1x^1+b_0}$$
dividir numerador y denominador por la mayor potencia de \(x,\) simplificar la expresión y aplicar propiedades de límites para realizar el cálculo, el resultado queda determinado como sigue:
Límites al infinito de funciones racionales.
\begin{align} &{\rm Si}~ m>n~~ {\rm se~ tiene}~~ \lim_{x\to\infty}{f(x)}=\infty ~~\therefore~~ {\rm no~ existe}\\ &{\rm Si}~ m< n~~{\rm se~ tiene~~} \lim_{x\to\infty}{f\left(x\right)}=0\\ &{\rm Si}~ m=n ~~{\rm se\ tiene} \ \ \lim_{x\to\infty}{f\left(x\right)}=\frac{a_m}{b_n}\end{align} Ver Ejercicios II del uno al cuatro.
Asíntotas horizontales y oblicuas de funciones racionales.
En algunos casos una función el comportamiento asintótico de una función es con una recta horizontal \(y=k\) donde k es una constante, un ejemplo esto es la gráfica de la función \(y=e^x\) que se muestra a la izquierda, la misma se acerca, se acerca a la recta \(y=0,\) pero nunca la toca. En tales casos se dice que la recta \(y=0\) es asíntota horizontal de la gráfica de \(y=e^x.\) Esto es debido a que si observa con atención la gráfica notará que a medida que \(x\) se hace más y más pequeña la función se acerca, más y más a la recta, es decir, $$\lim_{x\to\infty}{f\left(x\right)}=0,$$ este resultado no es una casualidad, sino más bien un caso particular de la siguiente definición.
Definición de asíntota horizontal (a.h.)
$${\rm Si}~\lim_{x\to\infty}{f\left(x\right)}=L ~~{\rm o~~} \lim_{x\to-\infty}{f\left(x\right)}=L$$ entonces la recta \(y=L\) es una asíntota horizontal de la gráfica de \(f(x).\)
Observe la similitud entre la definición informal del límite y la definición anterior, esto ayudará en su comprensión.
Determinación de una asíntota horizontal.
Si para una función racional \(f\) cualquiera el numerador y denominador son del mismo grado la función f tiene por asíntota horizontal la recta \(y=a/b\) donde \(a\) y \(b\) son los coeficientes principales del numerador y denominador, además si una función tiene asíntota horizontal no posee asíntota oblicua estas ocurren cuando el numerador es exactamente un grado mayor que el denominador, es la recta \(y=mx+n\) que resulta de realiza el cociente entre los polinomios. Mediante el uso del cálculo la pendiente m y el intercepto n están dados por,
Pendiente e intercepto de una asíntota oblicua.
$$m=\lim_{x\to\infty}{\frac{f\left(x\right)}{x}\ };\ \ \ \ \ \ \ \ \ \ n=\lim_{x\to\infty}{\left(f\left(x\right)-mx\right)} $$
Para más contenidos clic en y luego clic en la pestaña del contenido deseado.
Conclusiones finales.
Para finalizar con este análisis, recuerde que la existencia del límite está asociada a que la función se aproxime al mismo valor, cuando \(x\) tienda a un punto \(c\) tanto por la izquierda como por la derecha.
Un comportamiento distinto a esto, por la función garantiza la inexistencia del límite, el límite si existe es único y su determinación puede realizarse de tres maneras específicas: a) método tabular. b) método Gráfico. c) método analítico. Por último, recuerde que infinito no es número, es un concepto y por tanto un si el límite tiende a infinito no existe.
Para más contenidos clic en y luego clic en la pestaña del contenido deseado.
Analizar la existencia o no de, $$\lim_{x\to3}{f(x)}=\left\{\begin{array}{l} 4x-12, ~~{\rm si~~} x< 3\\ x^2 ~~~~{\rm si~~} x≥3\\ \end{array}\right.$$
Determinar el límite de la función por tramos en un punto indicado. $$\lim_{x\to{\frac{3}{2}}^+}{\left|2x-3\right|}-4$$
Determinar el límite de la función por tramos en el punto indicado. $$\lim_{x\to2}{{\rm g}(x)}=\left\{\begin{array}i5x+2~~{\rm si}~x>2\\4~~~~~~~~~{\rm si}~x=2\\16-2x~~{\rm si}~x< 2 \end{array} \right.$$
Una función por tramos con dos puntos indicados. Determinar el límite de la función por tramos siguiente en ambos puntos indicados. $$f(x)=\left\{\begin{array}i \frac{x^2+x-6}{x^2+3x-10}~~{\rm si}~x< 2\\ \frac{x^2+x-6}{3x^2-5x-2}~~{\rm si}~x\geq2\\ \end{array}~~~~{\rm en}~x_1=2~~{\rm y}~~x_2=-3\right.$$
Un límite que no existe. Determinar el límite de la función por tramos en un punto indicado. $$L=\lim_{x\to1}{f(x)}=\left\{\begin{array}ix^2+4~~{\rm si}~x\geq1\\3x+3~~{\rm si}~x< 1 \end{array} \right.$$
Una función por tramos con dos puntos indicados. Determinar el límite de la función por tramos siguiente en ambos puntos indicados. $$f(x)=\left\{\begin{array}i \frac{x^2+x-6}{x^2+3x-10}~~{\rm si}~x < 2\\ \frac{x^2+x-6}{x^2-5x-2}~~{\rm si}~x\geq2\\ \end{array}~~~~{\rm en}~x_1=2~~{\rm y}~~x_2=-3\right.$$
Asíntotas verticales. Determinar las asíntotas verticales de la función dada y luego usar el concepto de límites para confirmar el resultado de la función. $$f\left(x\right)=\frac{x^2-4}{x^3+3x^2-6x-8}$$
Límite al infinito. Sea \(k\) una constante cualquiera, entonces, $$\lim_{x\to\infty}{\frac{k}{x}}=\lim_{x\to\infty}{\frac{k}{x^2}}=\lim_{x\to\infty}{\frac{k}{x^3}}=\lim_{x\to\infty}{\frac{k}{x^r}}=0\ \ {\rm para}\ k\in\ \mathbb{R}$$
Usando factorización. Determinar el valor del límte (si existe), $$L=\lim_{x\to\infty}{\frac{\sqrt{9x^6-x}}{x^3+1}}$$
Una combinación de límites. Determinar el valor del límite, $$L=\lim_{x\to\infty}{\frac{\sqrt{9x^6-x}(2x^2-7x)}{(x^3+1)(1-x-x^2)}}$$
Asítotas de una función. Determinar todas las asíntotas para la función, $$y=\frac{5x^3+3x-5}{x^2-1}$$
Asíntotas de una función. Determinar todas las asíntotas de la función $$y=\frac{9x^2-7x+11}{3x^2-2x-1}$$
